本文探讨了关于从29个选项中选出7个的组合方式的复式计算问题。文章介绍了如何通过组合数学中的基本原理和方法来计算这种组合的数量，包括使用组合公式和计算工具的应用。文章还讨论了不同计算方法的优缺点，并强调了在实际应用中需要注意的问题，如避免计算错误和确保结果的准确性等。

在当今社会，随着科技的不断进步和数学理论的深入发展，各种复杂的计算问题逐渐浮出水面。“29选7复式计算”问题便是其中之一，本文将围绕这一主题展开讨论，介绍其背景、意义、计算方法以及实际应用等方面，以期为读者提供一个全面而深入的了解。

背景与意义

“29选7复式计算”问题源于组合数学中的组合问题，在统计学、计算机科学、金融等领域都有广泛的应用，从29个不同的元素中选出7个元素的所有组合方式有多少种，这就是一个典型的组合问题，通过解决这一问题，我们可以为相关领域提供有力的数学支持，推动科技进步和社会发展。

计算方法

解决“29选7复式计算”问题，我们需要用到组合数学中的组合公式，组合公式为：C(n,m)=n!/[m!(n-m)!]，其中n为总元素数量，m为选取的元素数量，!表示阶乘，在本问题中，n=29，m=7，我们需要计算C(29,7)。

直接计算阶乘和除法可能导致计算量大、精度损失等问题，我们可以借助计算机或数学软件来进行计算，这些工具可以迅速得出准确的结果。

数学原理分析

在计算过程中，我们涉及到了组合数学中的基本原理，组合是指从n个不同元素中取出m个元素（其中m≤n）的所有不同方式的数目，在本问题中，我们需要从29个元素中选出7个元素，不考虑选出的顺序，这就是一个典型的组合问题，通过计算组合数，我们可以得到所有可能的组合方式，这对于统计学中的样本抽取、金融中的投资组合等问题具有重要的应用价值。

实际应用场景分析

“29选7复式计算”问题在实际生活中有着广泛的应用，以下列举几个典型的应用场景：

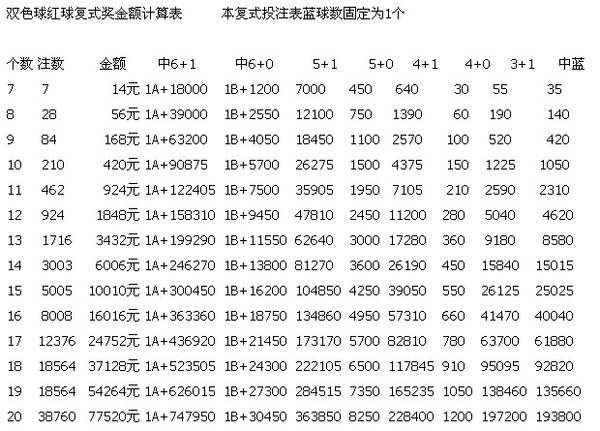
1、彩票行业：在彩票游戏中，我们经常需要从一定范围的数字中选择一定数量的数字进行投注，通过计算组合数，我们可以知道每个数字组合出现的概率，从而做出更明智的投注决策。

2、数据分析与挖掘：在大数据分析中，我们经常需要从大量的数据中选取一部分数据进行分析，通过计算组合数，我们可以知道有多少种不同的数据组合方式，从而更全面地了解数据的分布和特征。

3、金融投资组合：在金融领域，投资者经常需要从多种投资产品中选取一部分进行投资以分散风险，通过计算组合数，我们可以知道有多少种不同的投资组合方式，从而选择最优的投资策略。

4、生物学中的基因组合：在生物学研究中，基因的组合是一个重要的研究领域，通过计算组合数，我们可以了解基因组合的多样性和复杂性，为生物学研究提供有力的数学支持。

本文围绕“29选7复式计算”问题展开讨论，介绍了其背景、意义、计算方法以及实际应用等方面，通过深入了解我们发现，这一问题不仅涉及到数学中的组合原理，还在彩票、数据分析、金融投资等领域有着广泛的应用，随着科技的进步和社会的发展，我们将更加深入地研究这一问题及其相关应用，推动相关领域的发展，我们也期待更多的学者和研究者关注这一领域的发展，为科技进步和社会发展做出更大的贡献。